01 回归算法
一、理解线性回归模型
首先讲回归模型,回归模型研究的是因变量(目标)和自变量(预测器)之间的关系,因变量可以是连续也可以离散,如果是离散的就是分类问题。思考房价预测模型,我们可以根据房子的大小、户型、位置、南北通透等自变量预测出房子的售价,这是最简单的回归模型,在初中里面回归表达式一般这样写,其中x是自变量,y是因变量,w是特征矩阵,b是偏置。
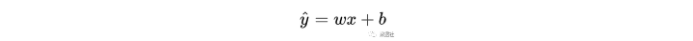
在机器学习推导里面引入线性代数的思想,将假设我们用一个表达式来描述放假预测模型,x代表一个房子的特征集,它是一个n×1的列向量,总共有m个特征集,θ是一个n×1的列向量,是我们想要求得未知数。
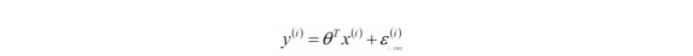
我们采用误差最小的策略,比如有预测表达式:y工资=Θ1*学历+Θ2*工作经验+Θ3*技术能力+.......+Θn*x+基本工资,预测的y值和实际值y_存有差距,策略函数就是使得m个特征集的(真实值y-预测值)的平方和最小。(差值可能是负数,所以采用平方和);
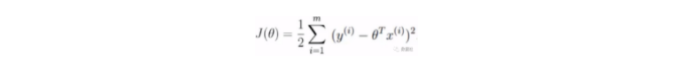
按照对于正规方程的求法,我们对θ 求偏导:
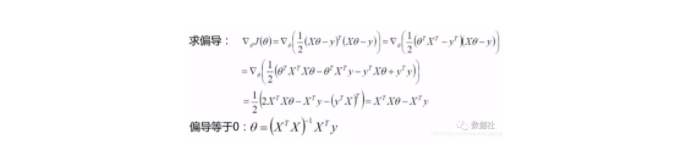
也就是,给定特征矩阵X和因变量y,即可以求使误差率最小的θ值,满足后续的回归模型。了解线性代数的童靴可以看出来问题,在θ的表达式中有求逆运算,需要保证矩阵可逆,这一般是无法保证的,这样就会造成θ无解,策略失效;
二、计算机的做法:梯度下降
常规的方程需要大量的矩阵运算,尤其是矩阵的逆运算,在矩阵很大的情况下,会大大增加计算复杂性。,且正规方程法对矩阵求偏导有一定的局限性(无法保证矩阵可逆),下面介绍梯度下降法,也就是计算机的解决方法,每次走一小步,保证这一小步是最有效的一步,可以想象自己正在下山,你不知道目的地(全局最小值)在哪,但是你能够保证自己每次走的都是最陡峭的一步;
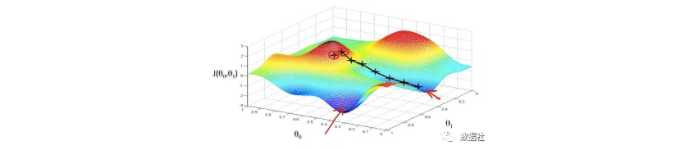
我们的策略仍然保持不变,就是使得m个特征集的(真实值y-预测值)的平方和最小:
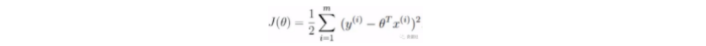
梯度下降法实现:赋予初始θ 值,并根据公式逐步更新θ 使得J(θ) 不断减少,最终至收敛,对应的参数θ 即为解。为了推导方便,首先研究只有一个训练样本时,如何计算推导公式。
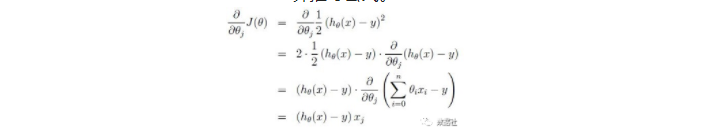
θ 的每个分量更新公式为:
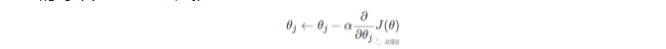
推广到m个训练数据,参数更新公式为:
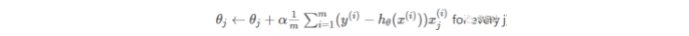
三、逻辑回归模型
逻辑回归与线性回归同属广义线性模型,逻辑回归是以线性回归为理论支持,是一个二分类模型,也可以推广多到分类问题,通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题,首先介绍一下Sigmoid函数:
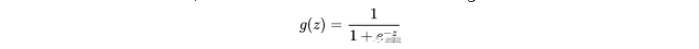
sigmoid函数图像是一个S曲线,取值在[0, 1]之间,在远离0的地方函数的值会很快接近0或者1,sigmoid函数的求导特性是:
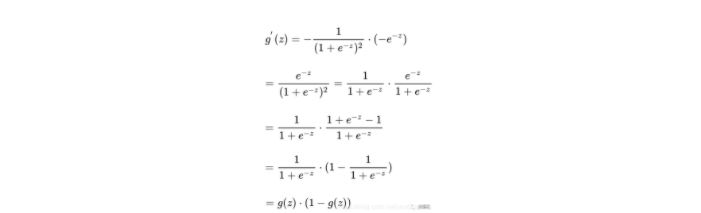
逻辑回归的预测函数是下图,只是在特征到结果的映射中加入了一层函数映射,先把特征线性求和,然后使用函数g(z)将最为假设函数来预测。g(z)可以将连续值映射到0到1之间:
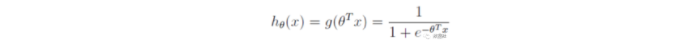
通过求似然函数,两边取log后,对θ求偏导:
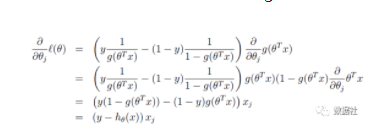
这样我们就得到了梯度上升每次迭代的更新方向,那么θ的迭代表达式为:
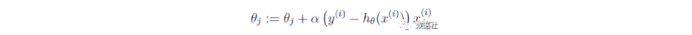
发现同线性回归模型是同一个表达式,这并不仅仅是巧合,两者存在深层的联系;
四、回归模型使用
数据是2014年5月至2015年5月美国King County的房屋销售价格以及房屋的基本信息。数据分为训练数据和测试数据,分别保存在kc_train.csv和kc_test.csv两个文件中,其中训练数据主要包括10000条记录,14个字段:销售日期,销售价格,卧室数,浴室数,房屋面积,停车面积,楼层数,房屋评分,建筑面积,地下室面积,建筑年份,修复年份,纬度,经度。
import pandas as pdfrom pandas import DataFrameimport numpy as npimport matplotlib.pyplot as plt%matplotlib inlineimport seaborn as snsfrom sklearn.linear_model import LogisticRegressionfrom sklearn.ensemble import RandomForestClassifierfrom sklearn.linear_model import LinearRegression# 数据读取baseUrl="C:\\Users\\71781\\Desktop\\2020\\ML-20200422\\houre_price\\"house_df=pd.read_csv(baseUrl+'train.csv' )test_df=pd.read_csv(baseUrl+'test.csv')house_df.head()
|
02 决策树
一、决策树算法理解
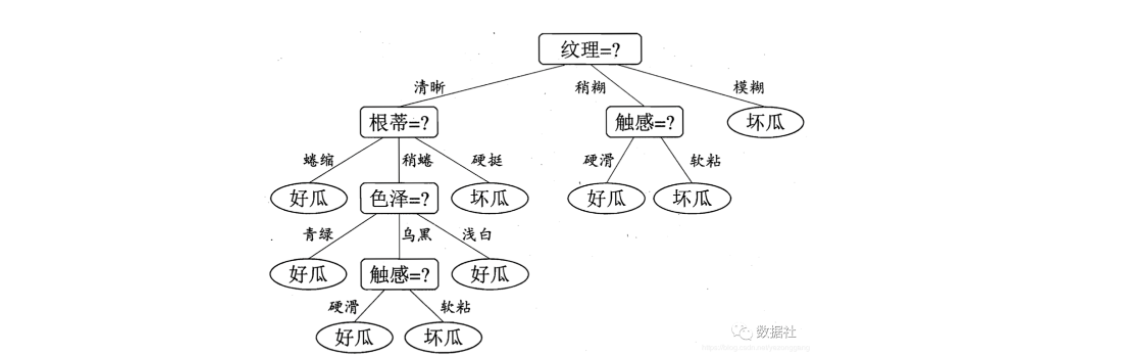
二、熵增益(ID3)
通信层面,信息熵衡量信息的不确定性,信息熵越大表明信息越不准确,可以用信息熵的减少值来衡量信息的价值。在决策树模型中把信息确定性叫做熵增益,有了熵增益后,我们就可以根据熵增益来判断特征值的重要程度,从而选取最重要的特征作为第一次切分,再根据相同的方法用其他特征进行切分,直到得到得到每个划分的叶子节点。信息熵的定义是:
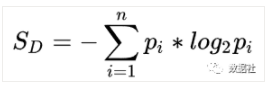
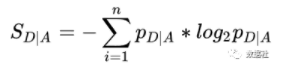
分类前的信息熵减去条件熵,得到熵增益:
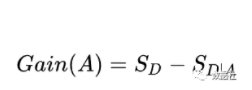
比如说有以下数据集(相亲结果表lol..)
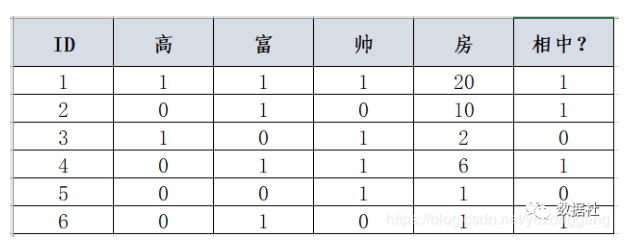
6条数据中相中(4个)与不想中(2个),暂且不关系如何进行分类,我们首先计算这个分类结果的信息熵:
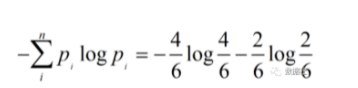
其次,我们计算“富”属性的条件信息熵,6条数据中“富”与否各半,其中3个“富”都被分类到“相中”,3个“不富”都被分到“不想中”:
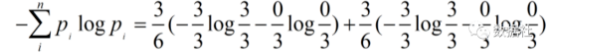
两者之差就是我们想要得到的熵增益:
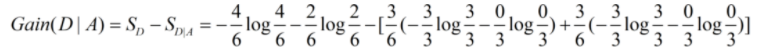
计算各个特征属性的熵增益后,比较哪个熵增益最大,就选择该属性做第一分类特征。
三、熵增益率(C4.5)
按照熵增益最大准则的ID3算法,遇到全部都是非重复值(类似ID)属性容易造成过拟合,因为如果根据ID这个属性进行划分发现此时的熵增益是最大的:
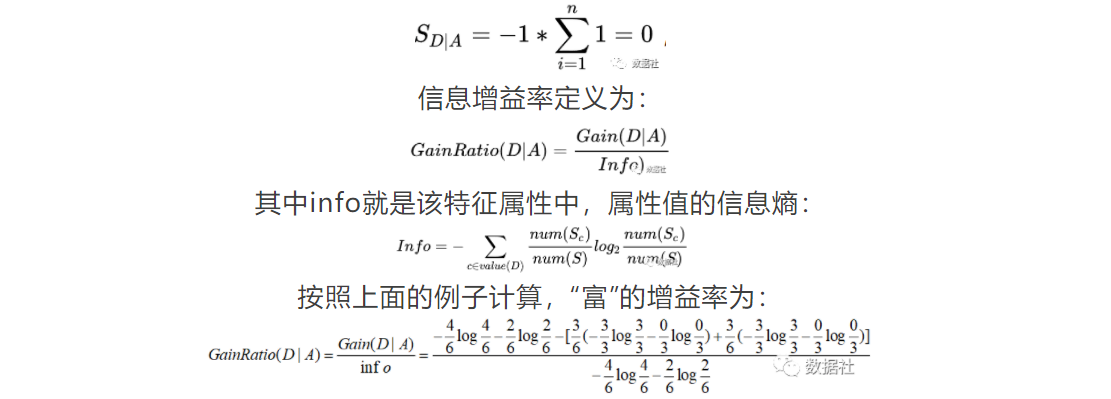
四、剪枝处理
五、鸢尾花(iris)分类模型
Iris 鸢尾花数据集是一个经典数据集,在统计学习和机器学习领域都经常被用作示例。数据集内包含 3 类共 150 条记录,每类各 50 个数据,每条记录都有 4 项特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度,可以通过这4个特征预测鸢尾花卉属于(iris-setosa, iris-versicolour, iris-virginica)中的哪一品种,数据集地址:https://github.com/yezonggang/iris
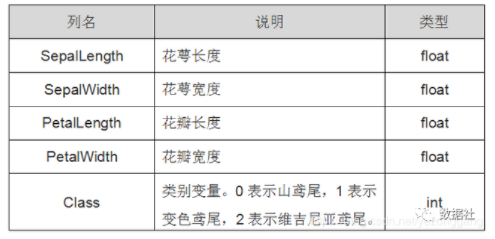
%matplotlib inlineiris_df.head()iris_df.describe()
|
数据分布探索:
# pandas 自带的散点图iris_df.plot(kind="scatter", x="Sepal.Length", y="Sepal.Width")
|
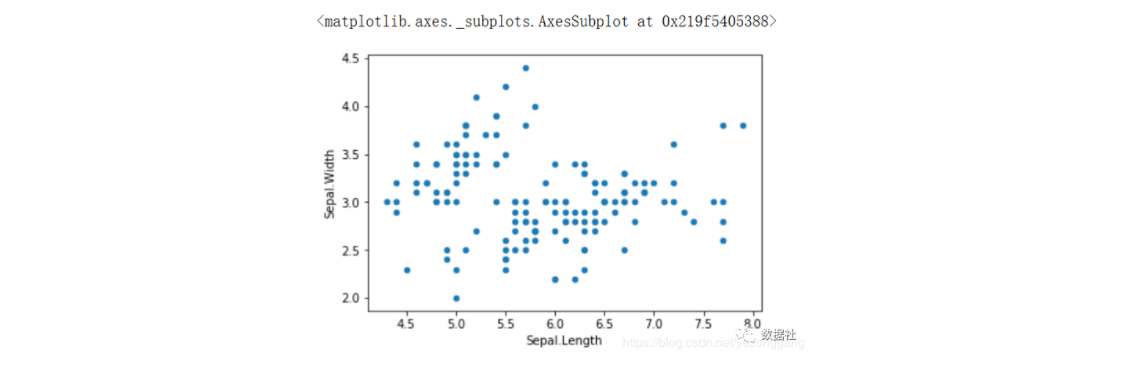
# seaborn 的联合分布图 sns.jointplot(x="Sepal.Length", y="Sepal.Width", data=iris_df, height=5)
|
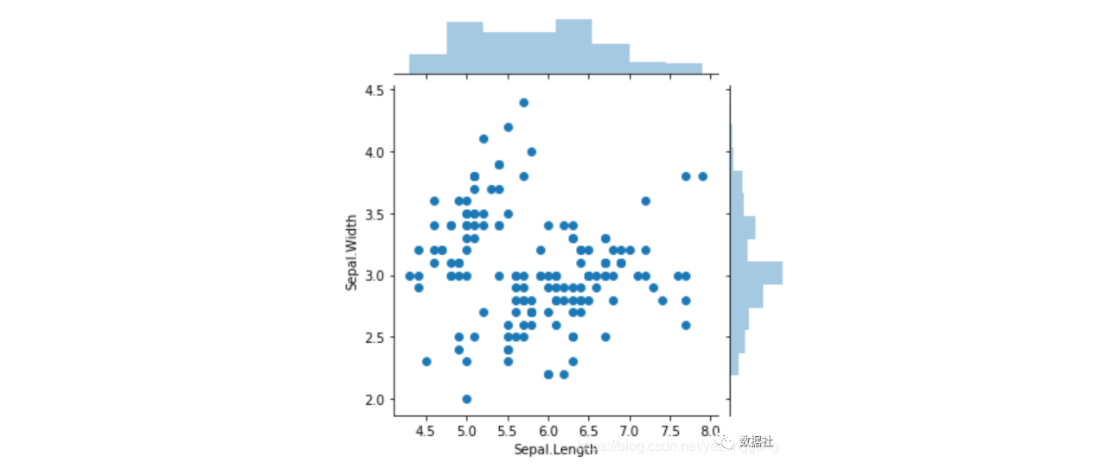
# 上面的两个散点图并不能显示每一个点所属的类别 # 所以,接下来用 seaborn 的 FacetGrid 函数按照Species花的种类来在散点图上标上不同的颜色,hue英文是色彩的意思。sns.FacetGrid(iris_df, hue="Species", height=5).map(plt.scatter, "Sepal.Length", "Sepal.Width").add_legend()
|
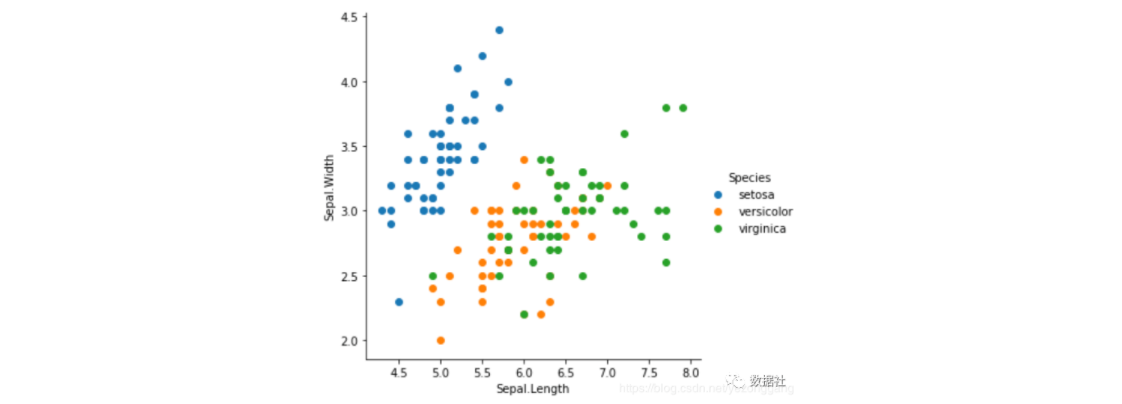
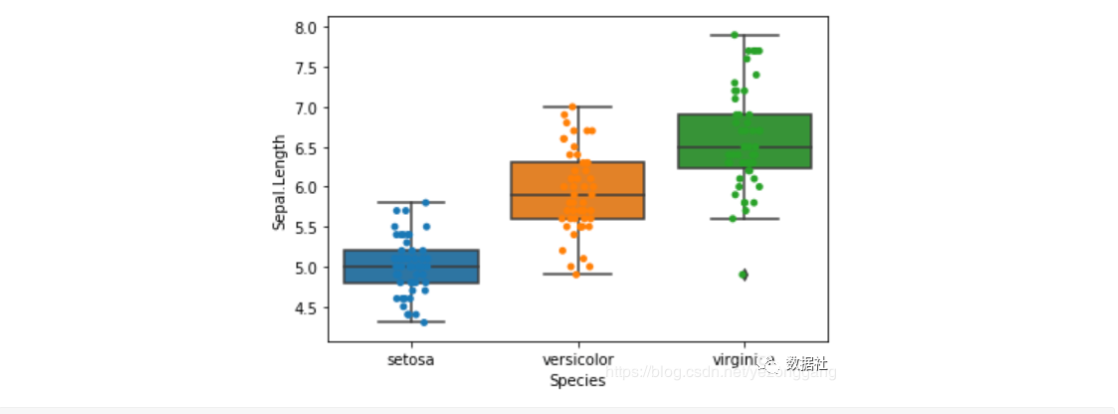
# 通过箱线图来查看单个特征的分布# 对 Numerical Variable,可以用 Box Plot 来直观地查看不同花类型的分布。sns.boxplot(x="Species", y="Sepal.Length", data=iris_df) |
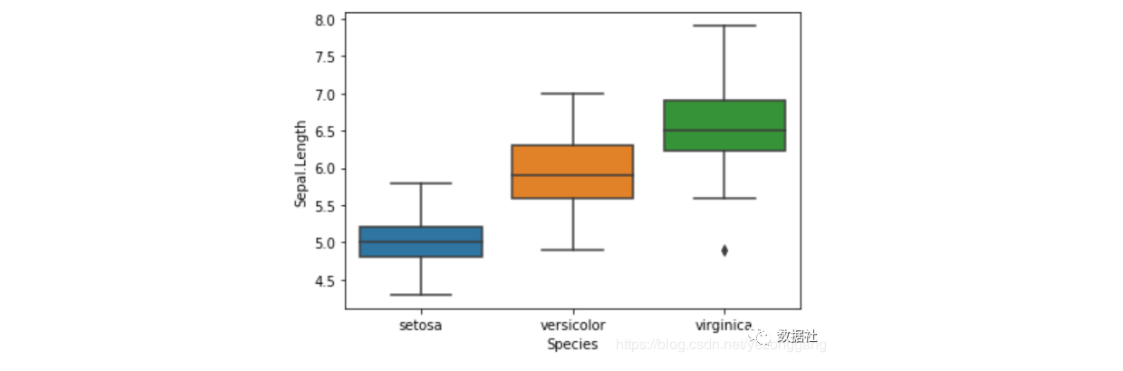
# 下面的操作,将每一个Species所属的点加到对应的位置,加上散点图,# 振动值jitter=True 使各个散点分开,要不然会是一条直线# 注意此处要将坐标图用ax先保存起来,这样第二次才会在原来的基础上加上散点图ax = sns.boxplot(x="Species", y="Sepal.Length", data=iris_df)ax = sns.stripplot(x="Species", y="Sepal.Length", data=iris_df, jitter=True, edgecolor="gray") |
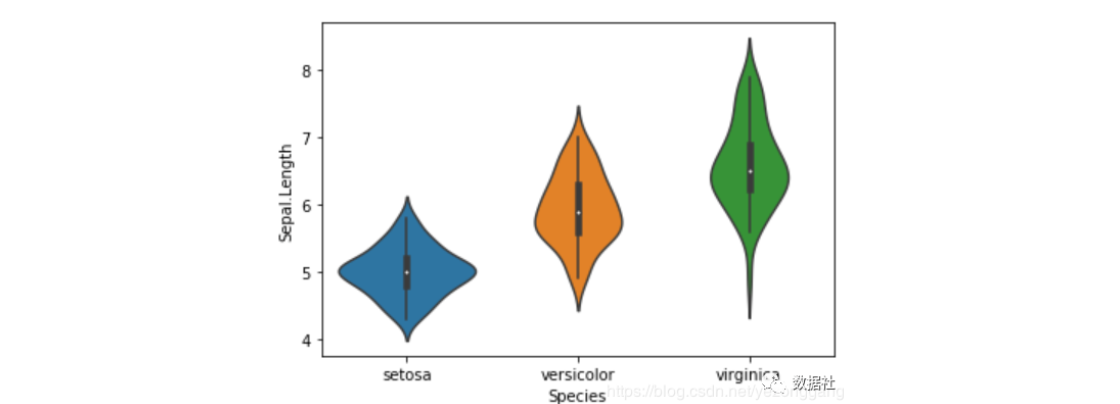
# violinplot 小提琴图,查看密度分布,结合了前面的两个图,并且进行了简化# 数据越稠密越宽,越稀疏越窄sns.violinplot(x="Species", y="Sepal.Length", data=iris_df, height=6) # sns.kdeplot == kernel density 核密度图(单个变量)sns.FacetGrid(iris_df, hue="Species", height=6).map(sns.kdeplot, "Sepal.Length").add_legend() # pairplot 任意两个变量间的关系sns.pairplot(iris_df, hue="Species", height=3)
|
#模型构建比较简单,关键是模型的调参 train_df=test_df=iris_df.sample(frac=0.8,replace=False, random_state=None)train_X=train_df.drop(['Species'],axis=1)train_Y=train_df['Species']# 由于么有提供建模数据集,所以我们随机从样本集中选择40%的数据集# replace=False 无放回的抽取# random-state 数据不能重复test_df=iris_df.sample(frac=0.9,replace=False, random_state=None)test_df.head()
|
1)分类策略:有两个参数 ‘entropy’(熵) 和 ‘gini’(基尼系数)可选,默认为gini。
2)max_depth(树的最大深度):默认为None,此时决策树在建立子树的时候不会限制子树的深度。也可以设置具体的整数,一般来说,数据少或者特征少的时候可以不管这个值。如果模型样本量多,特征也多的情况下,推荐限制这个最大深度,具体的取值取决于数据的分布。常用的可以取值10-100之间。
3)min_samples_split(分割内部节点所需的最小样本数):意思就是只要在某个结点里有k个以上的样本,这个节点才需要继续划分,这个参数的默认值为2,也就是说只要有2个以上的样本被划分在一个节点,如果这两个样本还可以细分,这个节点就会继续细分
4)min_samples_leaf(叶子节点上的最小样本数):当你划分给某个叶子节点的样本少于设定的个数时,这个叶子节点会被剪枝,这样可以去除一些明显异常的噪声数据。默认为1,也就是说只有有两个样本类别不一样,就会继续划分。如果是int,那么将min_samples_leaf视为最小数量。如果为float,则min_samples_leaf为分数,ceil(min _ samples _ leaf * n _ samples)为每个节点的最小样本数。
搞数仓也得懂几个常用机器学习算法下篇传送门:https://vip.kingdee.com/article/296327348473655808
文章来源:微信公众号【数据社】
发布于 数据智能 社群
推荐阅读

